Definición de determinantes
El determinante es una herramienta matemática, se puede encontrar o extraer un determinante únicamente de las matrices que son cuadradas (tienen igual número de filas y columnas), y es un numero real (en caso de que la matriz sea real) consistente en la suma de los productos elementales de la matriz.
El orden de un determinante viene dado por el número de filas y columnas que tenga. Existen diferentes métodos para resolverlos, que veremos a continuación.
Nota: Es necesario indicar que usaremos los símbolos Det(A) o │A│ para referirnos al determinante de A.
El determinante de una matriz puede ser positivo, negativo o cero.
EJEMPLO
Sabiendo que |A|=5, calcula los otros determinantes.
Solución
Tiene dos líneas proporcionales.
La tercera columna es igual a la suma de las otras dos.
Orden de una matriz determinantes
A cada matriz cuadrada A se le
asocia un número denominado determinante de A.
El determinante de A se denota por |A| o
por det (A).
A = 
Determinante de orden uno
|a 11| = a 11
|5| = 5
Determinante de orden dos
= a 11 a 22 -
a 12 a 21
Determinante de orden tres
Consideremos una matriz 3 x 3 arbitraria A = (aij).
El determinante de A se define como sigue:
=
= a11 a22 a33 +
a12 a23 a 31 + a13 a21 a32 -
- a 13 a22 a31 -
a12 a21 a 33 - a11 a23 a32.
=
3 · 2 · 4 + 2 · (-5) · (-2) + 1 · 0 · 1 -
- 1 · 2 · (-2) - 2 · 0 · 4 - 3 · (-5) · 1 =
= 24 + 20 + 0 - (-4) - 0 - (-15) =
= 44 + 4 + 15 = 63
Observe que hay seis productos, cada uno de
ellos formado por tres elementos de la matriz. Tres de los
productos aparecen con signo positivo (conservan su signo) y tres
con signo negativo (cambian su signo).
Matrices de orden inferior
El caso de matrices de orden inferior(orden 1, 2 o 3) es tan sencillo que si determinante se calcula con sencillas reglas conocidas. Dichas reglas son también deducibles del teorema de Laplace.
Una matriz de orden uno, es una caso trivial, pero lo trataremos para completar todos los casos. Una matriz de orden uno puede ser tratada como un escalar, pero aquí la consideremos una matriz cuadrada de orden uno:
Determinante de orden superior
El determinante de orden n, puede desarrollarse a partir de una fila o columna, reduciendo el problema al cálculo de un determinante de orden n-1. Para ello se toma una fila o columna cualquiera, multiplicando cada elemento por su cofactor (es decir, el determinante de la matriz que se obtiene eliminando la fila y columna correspondiente a dicho elemento, multiplicado por (-1)i+j donde i es el número de fila y j el número de columna). La suma de todos los productos es igual al determinante.
En caso de un determinante de orden 4, se obtienen directamente determinantes de orden 3 que podrán ser calculados por la regla de Sarrus. En cambio, en los determinantes de orden superior, como por ejemplo n = 5, al desarrollar los elementos de una línea, obtendremos determinantes de orden 4, que a su vez se deberán desarrollar en por el mismo método, para obtener determinantes de orden 3. Por ejemplo, para obtener con el método especificado un determinante de orden 4, se deben calcular 4 determinantes de orden 3. En cambio, si previamente se logran tres ceros en una fila o columna, bastara con calcular solo un determinante de orden 3 (ya que los demás determinantes estarán multiplicados por 0, lo que los anula). Para calcular el determinante de una matriz de 4x4 también se puede utilizar directamente la regla de Villalobos, que es una extensión de la regla de Sarrus.
La cantidad de operaciones aumenta muy rápidamente. En el peor de los casos (sin obtener ceros en filas y columnas), para un determinante de orden 4 se deberán desarrollar 4 determinates de orden 3. En un determinante de orden 5, se obtienen 5 determinates de orden 4 a desarrollar, dándonos 20 determinates de orden 3. El número de determinates de orden 3 que se obtienen en el desarrollo de un determinante de orden n es igual a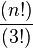 
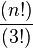
Por ejemplo, mediante este método, para un determinante de orden 10 se deberán calcular 10 x 9 x 8 x 7 x 6 x 5 x 4 = 604.800 determinantes de orden 3.
También puede utilizarse el Método de eliminación Gaussiana, para convertir la matriz en una matriz triangular. Si bien el proceso puede parecer tedioso, estará muy lejos de los 14.529.715.200 de determinantes de orden 3 necesarios para calcular el determinante de una matriz de orden 14
Determinante de orden infinita
Bajo ciertas condiciones puede definirse el determinante de aplicaciones lineales de un espacio vectorial de Banach de dimensión infinita. En concreto en el determinante está definido para los operadores de la clase de determinante que puede a partir de los operadores de la clase de traza. Un ejemplo notable fue el determinante de Fredholm que éste definió en conexión con su estudio de la ecuación integral que lleva su nombre:
(*)
Donde:
es una función conocida
es una la función incógnita
es una función conocida llamada núcleo, que da lugar al siguiente operador lineal compacto y de traza finita en el espacio de Hilbert de funciones de cuadrado integrable en el intervalo [0,1]:
:
La ecuación () tiene solución si el determinante de Fredholm 
no se anula. El determinante de Fredholm en este caso generaliza al determinante en dimensión finita y puede calcularse explícitamente mediante:
no se anula. El determinante de Fredholm en este caso generaliza al determinante en dimensión finita y puede calcularse explícitamente mediante:![\det(I+\hat{K}) = \sum_{k=0}^\infty \frac{1}{k!}\int_0^1\dots\int_0^1
\det[K(x_i,x_j)]_{1\le i, j \le k}\ dx_1\dots dx_k](https://upload.wikimedia.org/math/a/d/3/ad39f03c0adafbe3c5024fc8236d0a41.png)
La propia solución de la ecuación () puede escribirse de manera simple en términos del determinante cuando este no se anula.
Determinante de orden arbitrario
Sea A = (ann) una matriz de orden arbitrario n ´ n (siendo n un número par). Para calcular el det (A) se procede de la siguiente manera:
Los signos se van alternando según la posición que ocupen las entradas del determinante. Es decir:
EJEMPLO
Si observamos la matriz, podemos ver que en la tercera columna hay dos ceros. Así pues, si cogemos las entradas de la tercera columna para calcular el determinante, nos ahorraremos calcular dos determinantes, ya que el producto de un determinante por cero es cero.
= -1(-35) + 3(35) = 35 + 105 = 140.
Notación de determinantes
Notación matemática formada por una tabla cuadrada de números, u otros elementos, entre dos líneas verticales; el valor de la expresión se calcula mediante su desarrollo siguiendo ciertas reglas. Los determinantes fueron originalmente investigados por el matemático japonés Seki Kowa alrededor de 1683 y, por separado, por el filósofo y matemático alemán Gottfried Wilhhelm Leibniz alrededor de 1693. Esta notación se utiliza en casi todas las ramas de las matemáticas y en las ciencias naturales.
El símbolo
es un determinante de segundo orden, pues es una tabla con dos filas y dos columnas; su valor es, por definición, a11a22 - a12a21. Un determinante de orden n-ésimo es una tabla cuadrada con n filas y n columnas como se muestra en la figura:
El adjunto menor, Mij, de un elemento cualquiera aij de la tabla es el determinante formado por los elementos restantes al eliminar la fila i y la columna jen las que aparece el elemento aij. El cofactor, Aij, de un elemento aij es igual a (-1)i+jMij.
Propiedades de los determinantes
Los determinantes tienen las siguientes propiedades que son útiles para simplificar su evaluación.
En los párrafos siguientes consideramos que A es una matriz cuadrada.
Propiedad 1
Si una matriz A tiene un renglón (o una columna) de ceros, el determinante de A es cero.
EJEMPLO
Sea
Desarrollando por cofactores del primer renglón se tiene
Propiedad 2
con 
Esto es 
EJEMPLO
Sea
y 
con
y 
El producto
Y su determinante es
entonces
Propiedad 8
El determinante de la matriz identidad I es igual a 1 (uno)
EJEMPLOS
I =
det I = (1)(1) – (0)(0) = 1
Propiedad 9
El determinante de una matriz singular, es decir, que no tiene inversa, es igual a 0 (cero)
Los determinantes tienen las siguientes propiedades que son útiles para simplificar su evaluación.
En los párrafos siguientes consideramos que A es una matriz cuadrada.
Propiedad 1
Si una matriz A tiene un renglón (o una columna) de ceros, el determinante de A es cero.
EJEMPLO
Sea
Desarrollando por cofactores del primer renglón se tiene
Propiedad 2
El determinante de una matriz A es igual al determinante de la transpuesta de A.
esto es 
EJEMPLO
Sea 
La transpuesta de A es 
Propiedad 3
Si se intercambian dos renglones (o dos columnas) de una matriz A entonces el determinante cambia de signo.
EJEMPLO
sea 
con 
con
Intercambiando los renglones 1 y 2 la matriz queda
con
Note que los determinantes se calcularon expandiendo por cofactores de la primera columna.
Propiedad 4
Si una matriz A tiene dos renglones (o dos columnas) iguales entonces det A = 0.
EJEMPLO
Sea 
entonces 
entonces
Propiedad 5
Cuando un solo renglón (o columna) de una matriz A se multiplica por un escalar r el determinante de la matriz resultante es r veces el determinante de A, r det A.
EJEMPLO
Sea 
cuyo determinante se calculó en el ejemplo 2, 
cuyo determinante se calculó en el ejemplo 2,
Multiplicando el tercer renglón de A por el escalar r = 3 se tiene la matriz B siguiente
cuyo determinante, desarrollado por cofactores de la primera columna de B es
Propiedad 6
Si un renglón de la matriz A se multiplica por un escalar r y se suma a otro renglón de A, entonces el determinante de la matriz resultante es igual al determinante de A, det A. Lo mismo se cumple para las columnas de A.
EJEMPLO
Sea 
cuyo determinante se calculó en el ejemplo 2, 
cuyo determinante se calculó en el ejemplo 2,
Multiplicando la segunda columna de A por el escalar 2 y sumándola a la columna 3 se obtiene la matriz B siguiente
Expandiendo por cofactores de la primera columna se tiene
Propiedad 7
Si A y B son matrices de 
, el determinante del producto AB es igual al producto de los determinantes de A y de B.
, el determinante del producto AB es igual al producto de los determinantes de A y de B.EJEMPLO
Sea
y con
y El producto
Y su determinante es
entonces
Propiedad 8
El determinante de la matriz identidad I es igual a 1 (uno)
EJEMPLOS
I =
det I = (1)(1) – (0)(0) = 1Propiedad 9
El determinante de una matriz singular, es decir, que no tiene inversa, es igual a 0 (cero)
EJEMPLO
J = 
|J| = (1)(-12) – (-3)(4) = -12 +12 = 0
Se puede fácilmente comprobar que la matriz J no tiene inversa.
EJEMPLO
Calcular el determinante de la matriz A de
Simplificamos el cálculo del determinante de A reduciendo por renglones
Entonces, la permutación P14 cambia el signo de det A , las operaciones
y 
no cambian el valor del determinante.
De esta forma
Se podría seguir reduciendo a la forma triangular, pero observando que hay varios ceros en el tercer renglón resulta fácil desarrollar por cofactores, primero de la primera columna, y después del tercer renglón:
|J| = (1)(-12) – (-3)(4) = -12 +12 = 0Se puede fácilmente comprobar que la matriz J no tiene inversa.
Uso de las propiedades para calcular determinantes de alto orden.
Al utilizar las operaciones elementales sobre renglones, se puede reducir un determinante a una forma mas fácil de evaluar. Si se reduce a una forma triangular superior o inferior, el determinante es el producto de los elementos de la diagonal principal. Al hacerlo hay que tomar en cuenta las propiedades 3, 5 y 6, como en el siguiente ejemplo.
EJEMPLO
Calcular el determinante de la matriz A de
Simplificamos el cálculo del determinante de A reduciendo por renglones
Entonces, la permutación P14 cambia el signo de det A , las operaciones
y no cambian el valor del determinante.De esta forma
Se podría seguir reduciendo a la forma triangular, pero observando que hay varios ceros en el tercer renglón resulta fácil desarrollar por cofactores, primero de la primera columna, y después del tercer renglón:
Aplicación de la determinantes en la administración
= 
Son muchos los esfuerzos que realizan los gerentes de
pequeñas y medianas empresas por controlar los costos operativos y de
producción de sus empresas, como alternativa para crear ventajas sobre la
competencia (liderazgo en costos), y para incrementar o mantener el margen de
utilidad de la empresa, cuando los ingresos son constantes o difíciles de
incrementar, sin embargo, con frecuencia dichos esfuerzos son infructuosos,
dado que estos gerentes desconocen las verdaderas causas por las cuales la
empresa incurre en costos, ello induce a la toma de decisiones y al control de
costos de manera inadecuada, así como a reducciones arbitrarias, que atentan
contra la calidad y/u operativa de la empresa, tal vez porque atacan los
síntomas y no las verdaderas causas de dichos costos.
1)La ecuación de demanda de
cierto producto es:
p + 2 x = 25 y la ecuación de la oferta es:
p – 3 x = 5, en donde p es el precio y
x es la cantidad demandada o suministrada. Calcule los valores de x y p en el
punto de equilibrio de mercado.
La ecuación de demanda está dada: p + 2 x = 25
La ecuación de oferta está dada: p – 3 x = 5
Dónde: p: precio.
X: cantidad demandada o suministrada.
La matriz aumentada asociada al sistema está dada por:
Por lo tanto:
p = 7
x = 4
2. Una persona invirtió
un total de $ 20 000 en tres inversiones al
6, 8 y 10 %. El ingreso total anual fue de $ 1 624 y el ingreso de la inversión del
10 % fue dos veces el ingreso de la inversión al 6 %.
¿De cuánto fue cada
inversión?
Inversiones 1,2 y 3 respectivamente: I1, I2, I3.
Por condiciones del ejercicio se establece el siguiente
sistema de ecuaciones:
I1 (.06) + I2 (.08) + I3 (.10) = 1624
I1 + I2 + I3 = 20 000
2 I1 (.06) = I3 (.10)
La matriz aumentada asociada al sistema está dada por:
=
Por lo tanto la matriz aumentada asociada es
Por lo tanto
I1= $ 6 000
I2= $
6 800
I3= $
7 200
Referencias bibliográficas
Determinantes http://www.monografias.com/trabajos101/determinates-algebra-lineal/determinates-algebra-lineal.shtml
Determinantes http://www.monografias.com/trabajos101/determinates-algebra-lineal/determinates-algebra-lineal.shtml
Orden 1 2 3 http://www.ditutor.com/determinantes/determinante.html
Matrices de orden inferior ,superior
y infinita
Orden arbitrario http://www.sectormatematica.cl/contenidos/detordn.htm
Propiedades http://fcm.ens.uabc.mx/~matematicas/algebralineal/III%20Dets/propiedadesdets.htm
Ejercicio de la administración
http://www.monografias.com/trabajos101/ejercicios-tipo-matrices-y-determinantes/ejercicios-tipo-matrices-y-determinantes.shtml
Integrantes:
Grace Brito CI 24.228.896
David Pérez CI 20.078.138
Gabriela Mazzarri CI 26.748.458
Rules and How to play and get a bonus at baccarat
ResponderEliminarThe main difference between baccarat and other 1xbet korean casino games is that the bonus 바카라 사이트 is fairly small, and the payout rate is lower. In this, the bonus 인카지노